Hill climbing is one of the simplest optimisation algorithms. On a search graph one starts at a state, and then looks at neighbouring states choosing a better one and then shifting focus to that state. This step-by-step process is repeated until there are no neighbouring states that are better, at which point one has reached a local maximum, but not necessarily the global maximum. The simplest form of hill climb always chooses the very best neighbouring state, but if there are many neighbouring states, or when the search is over a continuous search space, it may be necessary to choose any good-enough next step that improves on the current state.
Note the name 'hill climbing' suggests that the optimal solutuon is the one with highest score, but there are also many applications where the smallest score is requred, for example, distance to a target state. In these case it is more like 'valley seeking', but the term 'hill climbing' is still applied. Note too that in some searches, particularly tree search some states are not goal states in themselves and so do not have a score or fitness as such, but instead have a heuristic value. In these cases one always moves to the best (or good enough) neighbour, even if this is actually worse than the heuristic of the current state.
Used on pages 72, 75, 116, 143, 179, 180, 187, 224
Also known as hill climbing, hill-climbing
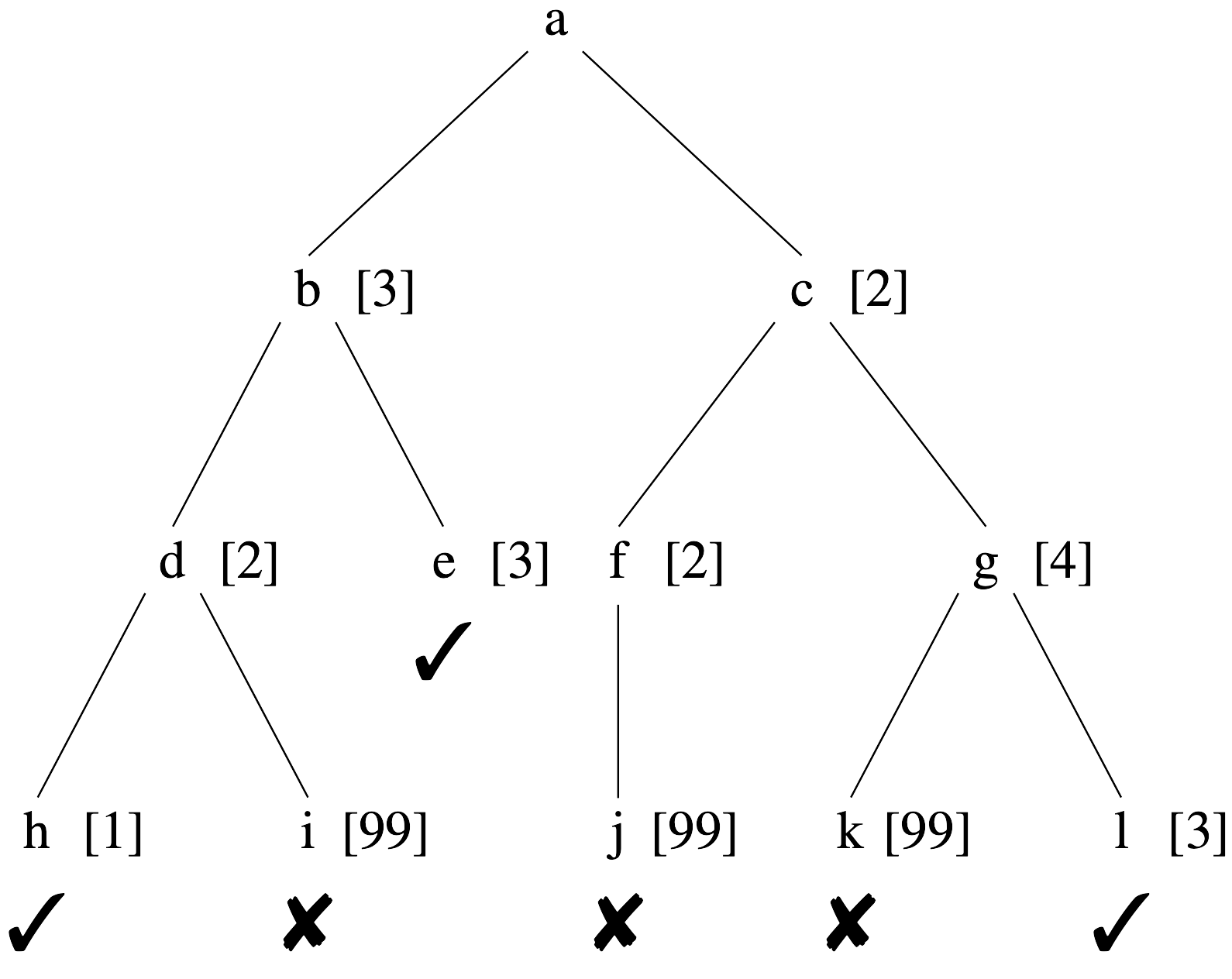
An example of 'hill climbing' on a search tree were the smallest solution is optimal. Hill climbing starting at the root a will visit c next as it has the lowest ({{heuristic}}) score between b and c. From c the best option is f and then j, but j is not an acceptable solution. {{Forgetful hill climbing}} will get stuck here, but {{hill climbing with backtracking}} would retry from g and then get to node l, which is a {{local minimum}}, but never get to node h, which is the {{ghlobal minimum}}.